I. Introduktion
Vand kan tænde lys, er det sandt? Det er sandt!
Er det sandt, at slanger er bange for realgar? Det er falsk!
Det vi skal diskutere i dag er:
Interferens kan forbedre målenøjagtigheden, er det sandt?
Under normale omstændigheder er interferens målingens naturlige fjende. Interferens vil reducere målenøjagtigheden. I alvorlige tilfælde vil målingen ikke blive udført normalt. Fra dette perspektiv kan interferens forbedre målenøjagtigheden, hvilket er forkert!
Men er dette altid tilfældet? Er der en situation, hvor interferens ikke reducerer målenøjagtigheden, men i stedet forbedrer den?
Svaret er ja!
2. Indblandingsaftale
Kombineret med den faktiske situation indgår vi følgende aftale om indblandingen:
- Interferensen indeholder ikke DC-komponenter. I den faktiske måling er interferensen primært AC-interferens, og denne antagelse er rimelig.
- Sammenlignet med den målte jævnspænding er interferensamplituden relativt lille. Dette stemmer overens med den faktiske situation.
- Interferens er et periodisk signal, eller middelværdien er nul inden for en fast tidsperiode. Dette punkt er ikke nødvendigvis sandt i den faktiske måling. Da interferensen generelt er et vekselstrømssignal med højere frekvens, er konventionen om nul middelværdi rimelig for de fleste interferenser over en længere tidsperiode.
3. Målenøjagtighed under interferens
De fleste elektriske måleinstrumenter og målere bruger nu AD-konvertere, og deres målenøjagtighed er tæt forbundet med AD-konverterens opløsning. Generelt har AD-konvertere med højere opløsning højere målenøjagtighed.
AD-opløsningen er dog altid begrænset. Hvis man antager, at AD-opløsningen er 3 bit, og den højeste målespænding er 8V, svarer AD-konverteren til en skala opdelt i 8 divisioner, hvor hver division er 1V. er 1V. Måleresultatet af denne AD er altid et heltal, og decimaldelen er altid ført eller kasseret, hvilket antages at være ført i denne artikel. At føre eller kassere vil forårsage målefejl. For eksempel er 6,3V større end 6V og mindre end 7V. AD-måleresultatet er 7V, og der er en fejl på 0,7V. Vi kalder denne fejl for en AD-kvantiseringsfejl.
For at lette analysen antager vi, at skalaen (AD-konverteren) ikke har andre målefejl bortset fra AD-kvantiseringsfejlen.
Nu bruger vi to identiske skalaer til at måle de to DC-spændinger vist i figur 1 uden interferens (ideel situation) og med interferens.
Som vist i figur 1 er den faktisk målte DC-spænding 6,3 V, og DC-spændingen i figuren til venstre har ingen interferens, og den er en konstant værdi. Figuren til højre viser jævnstrømmen forstyrret af vekselstrømmen, og der er en vis udsving i værdien. DC-spændingen i diagrammet til højre er lig med DC-spændingen i diagrammet til venstre efter eliminering af interferenssignalet. Den røde firkant i figuren repræsenterer konverteringsresultatet fra AD-konverteren.

Ideel DC-spænding uden interferens
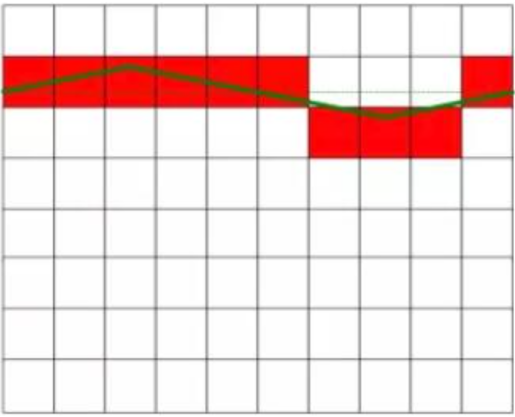
Påfør en interfererende jævnspænding med en middelværdi på nul
Foretag 10 målinger af jævnstrømmen i de to tilfælde i ovenstående figur, og beregn derefter gennemsnittet af de 10 målinger.
Den første skala til venstre måles 10 gange, og aflæsningerne er de samme hver gang. På grund af indflydelsen fra AD-kvantiseringsfejlen er hver aflæsning 7 V. Efter gennemsnittet af 10 målinger er resultatet stadig 7 V. AD-kvantiseringsfejlen er 0,7 V, og målefejlen er 0,7 V.
Den anden skala til højre har ændret sig dramatisk:
På grund af forskellen i den positive og negative pol af interferensspændingen og amplituden, er AD-kvantiseringsfejlen forskellig ved forskellige målepunkter. Ved ændring af AD-kvantiseringsfejlen ændrer AD-måleresultatet sig mellem 6V og 7V. Syv af målingerne var 7V, kun tre var 6V, og gennemsnittet af de 10 målinger var 6,3V! Fejlen er 0V!
Faktisk er ingen fejl umulige, for i den objektive verden er der ingen streng 6,3V! Der er dog:
I tilfælde af ingen interferens, da hvert måleresultat er det samme, forbliver fejlen uændret efter gennemsnittet af 10 målinger!
Når der er en passende mængde interferens, reduceres AD-kvantiseringsfejlen med en størrelsesorden efter at have beregnet gennemsnittet af 10 målinger! Opløsningen forbedres med en størrelsesorden! Målenøjagtigheden forbedres også med en størrelsesorden!
De vigtigste spørgsmål er:
Er det det samme, når den målte spænding har andre værdier?
Læserne kan følge aftalen om interferens i andet afsnit, udtrykke interferensen med en række numeriske værdier, lægge interferensen oven på den målte spænding og derefter beregne måleresultaterne for hvert punkt i henhold til AD-konverterens carry-princip og derefter beregne gennemsnitsværdien til verifikation, så længe interferensamplituden kan forårsage ændring af aflæsningen efter AD-kvantisering, og samplingsfrekvensen er høj nok (ændringer i interferensamplitude har en overgangsproces i stedet for to værdier: positiv og negativ), og nøjagtigheden skal forbedres!
Det kan bevises, at så længe den målte spænding ikke præcist er et heltal (den eksisterer ikke i den objektive verden), vil der være en AD-kvantiseringsfejl, uanset hvor stor AD-kvantiseringsfejlen er. Så længe interferensens amplitude er større end AD-kvantiseringsfejlen eller større end den minimale opløsning af AD, vil det medføre, at måleresultatet ændrer sig mellem to tilstødende værdier. Da interferensen er positiv og negativ symmetrisk, er størrelsen og sandsynligheden for fald og stigning ens. Derfor, når den faktiske værdi er tættere på hvilken værdi, er sandsynligheden for, at hvilken værdi vil vises, større, og den vil være tæt på hvilken værdi efter gennemsnittet.
Det vil sige: middelværdien af flere målinger (interferensmiddelværdien er nul) skal være tættere på måleresultatet uden interferens, det vil sige, at brug af AC-interferenssignalet med en middelværdi på nul og gennemsnittet af flere målinger kan reducere de ækvivalente AD-kvantiseringsfejl, forbedre AD-målingsopløsningen og forbedre målenøjagtigheden!
Opslagstidspunkt: 13. juli 2023




